Поиск значения лямбды в геометрии: методы и рекомендации

Лямбда – это часто используемый термин в геометрии и физике. Он означает величину, которая характеризует распределение каких-либо параметров в пространстве. Поиск лямбды имеет большое значение для решения различных задач, где требуется анализ и оптимизация. Найдем лямбду в геометрии!

Для того чтобы найти лямбду в геометрии, нужно знать определение и принципы работы с этой величиной. Во-первых, лямбда может быть использована для описания геометрической формы объекта или поверхности. Это связано с тем, что параметр лямбда определяет геометрические характеристики, такие как размер, форма, расположение и структура.

Во-вторых, для нахождения лямбды в геометрии часто используется анализ функций и уравнений, описывающих геометрические объекты. Например, функция распределения плотности может быть использована для нахождения доли площади под кривой или поверхностью, что позволяет найти соответствующую лямбду.

Наконец, для более сложных геометрических задач, таких как оптимизация формы или распределение параметров, могут применяться численные методы и моделирование. Эти методы позволяют не только найти лямбду, но и оптимизировать ее значение в соответствии с заданными условиями и ограничениями.

Понятие лямбды в геометрии

Лямбда может быть представлена числом, которое показывает компрессию или дилатацию объекта сравнительно с его исходными размерами. Положительное значение лямбды указывает на растяжение, в то время как отрицательное значение указывает на сжатие объекта.

Лямбда используется для изучения и анализа геометрических объектов, таких как эллипсы, окружности, эллиптические кривые и т.д. Эта величина позволяет определить, как объект будет изменяться при действии определенных трансформаций.

Примеры использования лямбды в геометрии:

1. В эллиптических кривых лямбда показывает, насколько будет растягиваться или сжиматься кривая при изменении параметров.

2. В трехмерной геометрии лямбда может использоваться для описания сжатия или растяжения объема фигуры.

Важно отметить, что значение лямбды может быть разным для разных осей или направлений в пространстве.

Лямбда представляет собой важный инструмент для изучения и анализа геометрических объектов, позволяющий определить их изменение в процессе различных преобразований.

Определение

Лямбда (λ) в геометрии используется для обозначения параметра, задающего положение точки на прямой или при преобразовании плоскости.

Параметр λ может быть любым числом в пределах от 0 до 1. Когда λ равно 0, точка находится в начале отрезка или до преобразования. Когда λ равно 1, точка находится в конце отрезка или после преобразования. Значение λ между 0 и 1 показывает пропорциональное положение точки на отрезке или после преобразования.

Используя лямбда в геометрии, можно выразить положение точки P на прямой AB с помощью формулы:

Параметрическое уравнение прямой:

P = A(1-λ) + Bλ

где:

• A и B — координаты начала и конца отрезка прямой
• P — координаты точки на прямой

Также лямбда может быть использована для обозначения пропорционального изменения при преобразовании плоскости. Например, при масштабировании точек можно использовать лямбда для нахождения новых координат точек после преобразования.

Способы нахождения лямбды

Существует несколько способов нахождения значения лямбды:

1. Метод векторов. Если даны уравнения двух прямых векторной параметрической форме, можно найти векторное уравнение прямой пересечения и определить значение лямбды из соответствующих координатного разложения.
2. Уравнение прямой. Если даны уравнения прямых в общем виде, можно составить систему уравнений и решить ее с помощью метода Крамера для нахождения значения лямбды.
3. Угловой коэффициент. Если известен угловой коэффициент прямых, можно использовать формулу для нахождения значения лямбды, основанную на равенстве углов.

В каждом из этих методов необходимо иметь начальные данные, такие как уравнения прямых или их характеристики. Точное значение лямбды позволяет более точно определить положение и свойства прямых в пространстве.

Обратите внимание, что значение лямбды может быть как числовым, так и символическим, в зависимости от конкретной задачи.

Метод поиска лямбды через углы

Для поиска значения лямбды в геометрии можно использовать метод, основанный на знании углов. Этот метод особенно полезен, когда имеется некоторое количество углов, относящихся к одной и той же дуге или сегменту окружности.

Для начала необходимо измерить заданные углы при помощи инструмента, например, угломера. Затем следует использовать геометрические свойства дуги или сегмента окружности, чтобы установить связь между измеренными углами и значением лямбды.

Если известны два угла, относящиеся к одной дуге, можно использовать свойство, согласно которому сумма мер дуги и ее сегмента составляет 360 градусов. Например, если измеренные углы равны 60 и 120 градусов, можно записать уравнение:

60° + 120° + λ = 360°

Далее, нужно решить полученное уравнение относительно λ:

λ = 360° — 60° — 120°

λ = 360° — 180°

λ = 180°

Таким образом, значение лямбды равно 180 градусов.

Этот метод можно применять и для других задач, связанных с геометрией, где требуется найти значение лямбды. Он позволяет использовать известные углы для определения значения лямбды и дальнейшего решения геометрической задачи.

Метод нахождения лямбды по сторонам треугольника

Для нахождения лямбды по сторонам треугольника нужно выполнить следующие шаги:

1. Найдите длины всех сторон треугольника.
2. Вычислите площадь треугольника с помощью формулы Герона или другим способом.
3. Возведите каждую длину стороны в квадрат.
4. Разделите каждый квадрат стороны на площадь треугольника.

После выполнения этих шагов вы получите значения лямбды для каждой стороны треугольника. Обычно лямбду обозначают символом λ.

Знание лямбды позволяет решать различные задачи геометрии, такие как нахождение радиусов вписанных и описанных окружностей, построение и нахождение площади подобных треугольников и многое другое.

Метод геометрического анализа в поиске лямбды

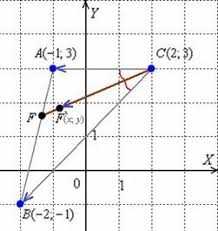
Шаг 1: Анализ исходных данных

Первым шагом для поиска значения лямбда требуется анализировать исходные данные задачи. Это могут быть заданные координаты точек, уравнения прямых или плоскостей, длины отрезков и другие геометрические параметры. Важно внимательно изучить и уяснить все имеющиеся данные, чтобы правильно приступить к решению задачи.

Шаг 2: Применение геометрических свойств

После анализа исходных данных необходимо применить геометрические свойства и отношения в задаче. Часто задачи в геометрии требуют использования теорем, правил и формул. При применении этих свойств можно получить уравнения, из которых можно выразить значение лямбда.

Например, если задача связана с поиском точки пересечения двух прямых, можно воспользоваться условием, что координаты искомой точки должны удовлетворять уравнению каждой из прямых. Подставив в уравнения координаты точки, можно выразить значение лямбда.

Шаг 3: Решение уравнений и поиск лямбды

После применения геометрических свойств и получения уравнений можно перейти к решению этих уравнений и поиску значения лямбда. Для этого может потребоваться применение алгоритмов решения систем уравнений или простых алгебраических методов.

После нахождения значения лямбда можно использовать его для решения исходной задачи или для получения дополнительной информации о геометрическом объекте.

Таким образом, метод геометрического анализа является эффективным инструментом в поиске значения лямбда в геометрии. Правильное применение геометрических свойств, анализ исходных данных и решение уравнений позволяют успешно найти требуемое значение и применить его для решения задачи.

Практическое применение лямбды

1. Построение и анализ кривых

Лямбда может быть использована для построения и анализа различных кривых в геометрии, таких как эллипсы, гиперболы и параболы. Она может помочь определить форму и особенности данных кривых, такие как фокусное расстояние, эксцентриситет и точки перегиба.

2. Графическое моделирование

Лямбда может быть использована в компьютерной графике и графическом моделировании для создания различных эффектов и анимаций. Например, она может быть использована для анимации движения объектов по траектории, определенной кривой с заданным значением лямбды.

Значение лямбды может меняться в зависимости от времени или других параметров, что позволяет создавать интересные и динамичные визуальные эффекты.

Все вместе, эти примеры демонстрируют широкий спектр применений лямбды в геометрии и связанных областях. Использование лямбды может помочь визуализировать и анализировать геометрические формы и помочь в создании интересных и динамичных визуальных эффектов.

Приложение лямбды в реальной жизни

1. Функциональное программирование: лямбды часто используются для создания анонимных функций, которые могут быть переданы другим функциям или сохранены в переменных. Это позволяет писать более компактный и эффективный код.
2. Параллельное программирование: лямбды позволяют создавать асинхронные задачи и обрабатывать их параллельно. Это особенно полезно при работе с большими объемами данных или при выполнении задач, требующих множественных вычислений.
3. Работа с событиями: лямбды позволяют легко обрабатывать события в приложениях. Они могут быть использованы вместо отдельных методов обработки событий, что делает код более читаемым и удобным в поддержке.
4. Работа с коллекциями данных: лямбды могут быть использованы для фильтрации, сортировки и преобразования данных в коллекции. Это делает работу с данными более гибкой и удобной.
5. Алгоритмы и оптимизация: лямбды могут быть использованы для реализации различных алгоритмов и оптимизации кода. Они позволяют писать более эффективные и компактные решения для различных задач.

Таким образом, лямбды имеют широкий спектр применения в реальной жизни. Они позволяют писать более гибкий и эффективный код, упрощают разработку и обслуживание приложений, а также способствуют оптимизации различных процессов. Поэтому понимание и использование лямбды становится все более важным для разработчиков и программистов в различных областях.